合作客戶/
拜耳公司 |
同濟大學 |
聯合大學 |
美國保潔 |
美國強生 |
瑞士羅氏 |
相關新聞Info
氣泡液體中的演變動力學分析
來源:知乎 阿黃sweetgirl 瀏覽 797 次 發布時間:2021-08-21
氣泡液體是大小不同的球狀氣泡分散到液體中的液氣體系。在氣泡液體中,大小不同氣泡是一個不穩定的體系,其內部不等的壓強會使整個體系變化,總體趨勢是氣泡半徑出現粗化現象,這種粗化跟晶體生長中的Ostwald熟化的現象是一致的(Ref 1)。根據附加壓力公式,可知較小的氣泡其內部具有較大的壓強,因此與旁邊較大的氣泡間就會存在壓強差(圖1a),氣泡間液體兩側的壓強差會使氣體從壓強較大的地方向較小的地方擴散,從而出現大的氣泡增大,小的氣泡減小直至消失的情形,這就是氣泡Ostwald熟化的機理(Ref 2)。從能量的觀點來說,Ostwald熟化的結果降低了體系的表面能,從而使整個體系更加穩定。
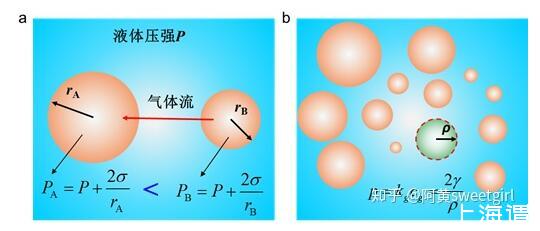
圖1(a)氣泡演變Ostwald熟化原理(b)Lemlich理論中半徑為ρ的假想氣泡模型
從定性的角度來看,氣泡的Ostwald熟化的過程是大氣泡吸收小氣泡的過程。但從定量上的角度來說,在氣泡演變的任一時刻,到底尺寸為多少的氣泡傾向為長大,而尺寸為多少的氣泡減小而傾向于消失呢?1978年,美國辛那提大學的Robert Lemlich建立模型解決了這個問題(Ref 3)。Lemlich的理論核心和依據是:1)假設所有的氣泡內的液體相互擴散時,都是先把氣體擴散到液體中,再通過液體擴散到其他氣泡中實現Ostwald熟化過程(圖1a),這個假設在氣泡含量不高,不是相互接觸的情形下是合理的。2)在氣泡演化的任何一個時刻,液體中氣體的濃度是均勻一致的,這個假設在研究所有氣泡的演化整體行為上是可行的。3)依據亨利定律,這個液體中氣體的濃度可以等價為液體內部有一個氣體壓強,而這個壓強可以看成是一個假想的氣泡內部的壓強(圖1b),其半徑ρ可以依據Laplace方程計算出來。所以,所謂氣泡演化就是所有氣泡跟這個假想的氣泡進行氣體交流。這樣就把體系中氣泡演變多對多擴散的復雜情形簡化為了多對一的演變過程。由此,體系中任意一個半徑為r氣泡與這個液體的中假想的氣泡的壓強差△P為
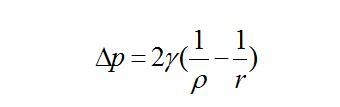
公式1
此氣泡與液體(假想氣泡)之間的氣體的以摩爾為單位的傳輸速率Qm為

公式2
公式中J為氣體的有效滲透系數,As為氣泡氣體傳輸發生的表面積,dn/dt是單位時間傳輸的摩爾數。對于球形氣泡As=4πr^2,在任一時刻,通過所有氣泡界面的氣體量是守恒的,即
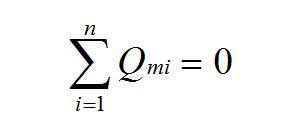
公式3
假設氣體符合氣體理想氣體方程,即PV=nRT,對于球形氣泡,體積V=4πr^3/3,從而可把摩爾速率轉化為氣泡半徑變化的速率。通過以上各式,可得
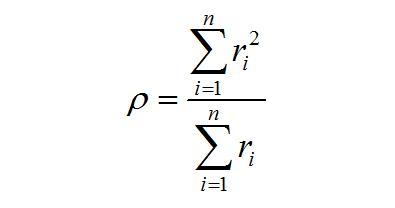
公式4
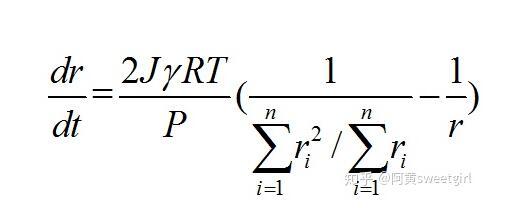
公式5
這就給出了氣泡Ostwald的動力學方程。對于任意氣泡體系,知道某時刻的氣泡體積或者半徑分布,就可以利用公式4算出ρ判定體系中的氣泡是增大還是減小,氣泡半徑大于ρ的在這一時刻又增大的趨勢,小于的會在下一時刻減小,根據ρ的公式,其含義是所有氣泡的瞬時平均半徑。而且,利用公式5就可以預測氣泡在后面任意時刻的氣泡分布,以及氣泡的演化的最終狀態及所需要的時間。
Lemlich的理論在預測低含量的氣泡時的演化規律無疑是合理而準確的。而且氣泡含量越低,其準確性越高。最重要的原因他的理論建立在氣體傳輸發生在氣泡與液體而不是氣泡與氣泡之間。對于高濃度的氣泡液體,氣泡之間相互擠壓,氣體傳輸可以直接通過氣泡接觸的邊界進行。而且在演化中,液體的局域氣體濃度也不全相同,在預測這類演化時,會出現較大的誤差,需要用到泡沫的結構與演化規律去解釋。
筆者借用這種理論,討論了在微結構下氣泡的演變行為。并去控制氣泡的演變過程和演變方向,其相應結果發表在Ref4中。控制演變過程的動畫如下所示:

微結構下氣泡演變的集聚效應
即剛開始無序的氣泡,在生長和微結構的調控下,最終全部演變為正十二邊形的規則氣泡陣列。
Ref 1:Lifshitz,I.M.&Slyozov,V.V.The Kinetics Of Precipitation From Supersaturated Solid Solutions.J.Phys.Chem.Solids 19,35-50(1961).
Ref 2:Stevenson,P.Inter-bubble gas diffusion in liquid foam.Curr.Opin.Colloid Interface Sci.15,374-381(2010).
Ref 3:Lemlich,R.Prediction of Changes in Bubble Size Distribution Due to Interbubble Gas Diffusion in Foam.Ind.Eng.Chem.Fundam.17,89-93(1978).
Ref 4:Zhandong Huang,Meng Su,Qiang Yang,Zheng Li,Shuoran Chen,Yifan Li,Xue Zhou,Fengyu Li,Yanlin Song*.A general patterning approach by manipulating the evolution of two-dimensional liquid foams.Nat.Commun.2017,8,14110.
注:此文摘選自本人博士畢業論文。










