合作客戶/
拜耳公司 |
同濟大學 |
聯合大學 |
美國保潔 |
美國強生 |
瑞士羅氏 |
相關新聞Info
一滴水緩慢落到非常光滑的平面上,接觸面積會有多大?
來源:知乎 阿黃sweetgirl 瀏覽 1403 次 發布時間:2021-07-29
此問題中,其實絕對光滑不太合適,一般可以考慮原子級別的光滑就已經可以使用(或可以看做沒有接觸角滯后現象)。為了讓解析式簡便,此題轉化為:
如果將體積為V的液體水滴落到原子級別光滑的光滑固體表面上,設固體表面對水的接觸角為θ,那么液滴穩定后,液滴與固體之間的接觸面積S有多大?
下面我僅僅使用參數V和θ,以及水的物性常數找出S的簡單解析式。
首先,此題必須分為兩種情形。第一種,是液體V很小時,此時表面張力占主導地位。此解法宮非前輩已經給出,但是其解析式不夠簡化。因此我進一步加以簡化。當表面張力占主導時,液滴成完美的球缺狀,如圖1所示。
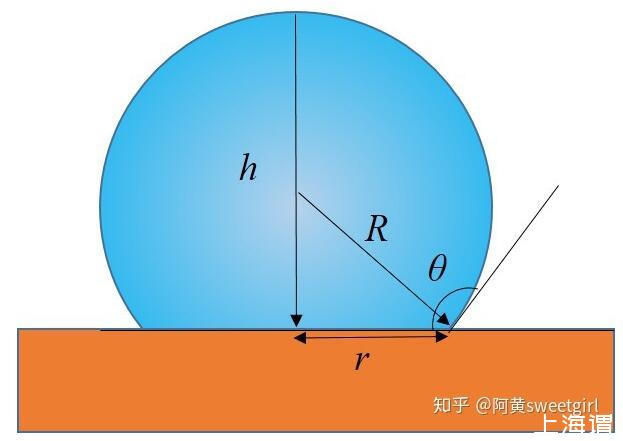
圖1液體體積很小時,毛細作用力占主導的情形,液滴呈球形
此時根據球的體積公式,以及簡單的三角函數變換,就可以得出S與V和θ的關系,具體推導過程如圖2所示。
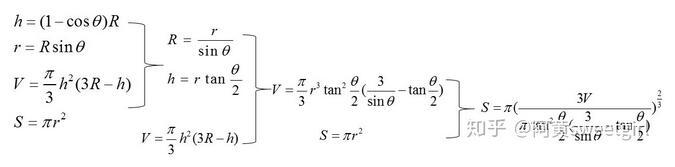
圖2接觸面積S的推導過程
此時可以看出,S與V的2/3次方是正比例關系。對于自然界任何光滑的表面,接觸角處于0到122°的范圍內,可以繪出S與θ的關系,如圖3所示。
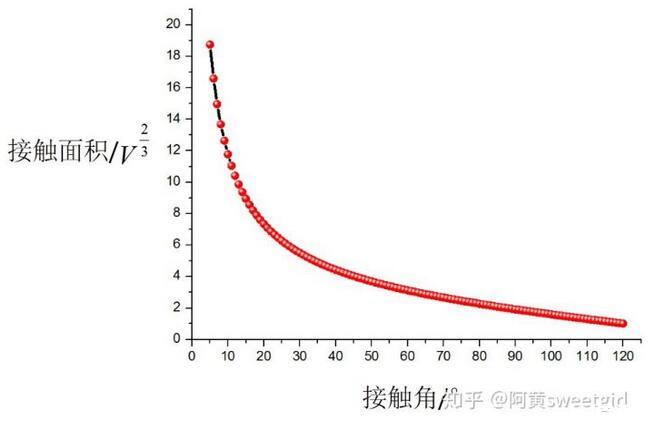
圖3接觸面積隨著接觸角的變化關系
上圖是接觸角從5°到120°范圍內的接觸面積的變化關系,基本上涵蓋了自然界中的大多數物質的光滑固體表面。
然后再是第二種情形,就是液體體積很大,此時表面張力很弱,重力占主導地位的場景。此時,液滴在光滑固體表面的呈現出扁平狀。如圖4所示。

圖4液體體積很大的情形
有意思的是,已經有前人對這種情形做過詳細的受力分析。得出只要接觸角一定,此時無論加多少水,液體的厚度e都不會增加,只會增加鋪展的面積。其厚度e的表達式為:
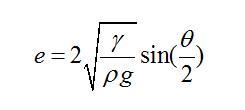
式中,γ為表面張力,p為密度,g為重力加速度。
由于此時,表面張力影響很小,液膜可以看成均勻的厚度,所以滿足
V=Se
從而可以推出:
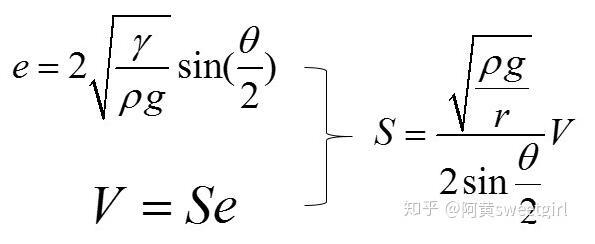
圖5液體接觸面積的推導公式。
至于具體的推導e的過程,可以見如下分析:


參考文獻:Capillarity and Wetting Phenomena書籍。










