合作客戶/
拜耳公司 |
同濟大學 |
聯合大學 |
美國保潔 |
美國強生 |
瑞士羅氏 |
相關新聞Info
推薦新聞Info
-
> 拉脫法測量:不同性能磁性液體的磁表面張力變化規律與影響因素(二)
> 拉脫法測量:不同性能磁性液體的磁表面張力變化規律與影響因素(一)
> 表面張力和接觸角對塑料熔體在微型通道內的流變行為的影響(二)
> 表面張力和接觸角對塑料熔體在微型通道內的流變行為的影響(一)
> 表面張力的生物醫學領域的具體應用
> 內壓力是什么意思?液體表面張力與內壓力的區別與定量關系
> 不同溫度下陰-非離子雙子星座表面活性劑表面張力的變化
> 常見多元醇(乙二醇、甘油、季戊四醇、山梨醇等)在化妝品中的作用
> 山茶油改性方法、制備原理及在水劑型化妝品中的應用(二)
> 山茶油改性方法、制備原理及在水劑型化妝品中的應用(一)
液體表面的表面張力會拉動泡泡,讓其表面積盡可能的小
來源:返樸 瀏覽 909 次 發布時間:2022-06-02
自然界中有不少神奇現象令人震撼,你能想到蜂巢、肥皂泡和海綿外骨骼之間的奇妙聯系嗎?答案是它們鐘愛六邊形。為何蜜蜂會打造出完美的六邊形蜂巢?這當然不是什么神秘的力量,而是其中富含的深刻數學和物理學道理。
Part.1 蜜蜂,天生的數學家?
蜂巢簡直是個工程學奇跡:它由一排排棱鏡似的“小隔間”組成,每一個“小隔間”的橫截面都是完美的六邊形;由蜂蠟制成的墻壁,每一面的厚度都相當精確;所有的房間沿水平方向微微傾斜,不僅避免蜂蜜從蜂巢里流出來,還讓整個蜂巢的方向與地球磁場方向一致。
蜜蜂在動工之前并沒有做過統籌規劃,也不可能拿到設計圖紙,它們卻能分工合作,鬼使神差地完成了如此精妙絕倫的蜂巢。
蜜蜂是怎么做到的?
古希臘哲學家帕普斯(Pappus of Alexandria)認為,蜜蜂一定天賦異稟,有著“幾何學的遠見卓識”。那么,又是誰給了它們這種遠見卓識,似乎只能是上帝吧?莫非蜜蜂果真像威廉·柯比(William Kirby)在1852年說的那樣,是“天生的數學家”?不管你信不信,反正達爾文不信。達爾文認為主導這一切的是進化論,而不是什么神祗的力量,于是他進行了一系列實驗,想證實蜜蜂是否僅憑進化和遺傳得來的本能就可以建造出完美的蜂巢。
下一個問題是,為什么是六邊形?這其實是一個很簡單的幾何問題。假設我們想用相同形狀和大小的圖形密鋪一個平面(使圖形不留空隙、也不互相重疊地鋪滿整個平面),那么只有3種正多邊形可以做到:正三角形、正方形和正六邊形。(這里指規則鑲嵌。關于不規則鑲嵌可參見《彭羅斯:不思考生物化學的諾貝爾物理學獎得主不是好的數學家》。)在鋪滿同等面積的情況下,使用正六邊形所需要的周長之和最小。這就不難理解蜜蜂為什么會選擇六邊形了,因為蜂巢是用蜂蠟做的,而蜜蜂產出蜂蠟是消耗能量的,它們當然希望省些力氣——這點小心思就跟打工人想少搬幾塊磚一樣。
人們早在18世紀就明白了這一點,用達爾文的話說,六邊形的蜂巢是“最省勞動力、也最省材料的選擇”。他認為,既然六邊形蜂巢所需要的能量和時間是最少的,那么在自然選擇的作用下,這種建造方式就成了蜜蜂的本能。不過,就算蜜蜂真的會測量巢房的角度,會測量墻壁的厚度,它們也未必需要依賴這種本能。因為,創造六邊形是大自然一貫的做法。
Part.2 大自然更愛“斤斤計較”
如果你在水面上吹一層泡泡——也就是“泡泡筏(Bubble raft)”——這些泡泡最后都會變成六邊形或者近似于六邊形的形狀。你不可能看到有哪個泡泡筏里全是正方形的泡泡,如果有4個泡泡聚集在了一起,它們會馬上重新排列成“三足鼎立”的樣子,交界處就像經典的奔馳標志,三邊相接,夾角差不多都是120°。
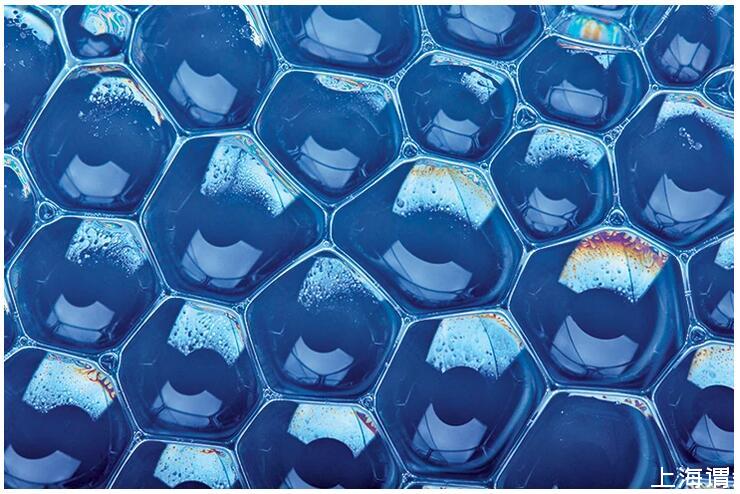
單層的“泡泡筏”由大多數六邊形(不一定是正六邊形)的泡泡組成。有一些“缺陷”泡泡可能有五面或七面。但三邊相交,角度約為120°。圖源:Shebeko/Shutterstock
蜂巢中的六邊形尚且有個“幕后推手”——說的就是蜜蜂,而泡泡筏中的六邊形可并沒有什么神秘力量在驅使。如果硬要說有,那么這個神秘力量就是物理學規則。(參見《數理史上的絕妙證明:簡單泡泡背后的恐怖數學》)
如果我們從平面的泡泡筏推演到立體的“泡泡堆”,結果也是類似的。假如你用吸管對著一碗肥皂水吹氣,吹起一堆泡沫,你會看到,當泡泡堆積在一起之后,它們四面邊界相交于一個點,夾角約為109°——沒錯,這個角度就是正四面體中心到各頂點連線的夾角。
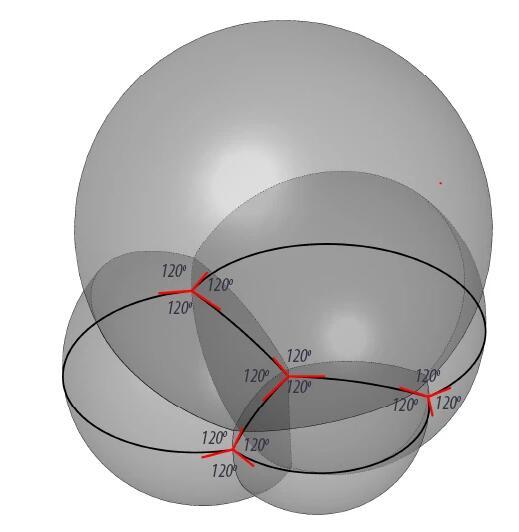
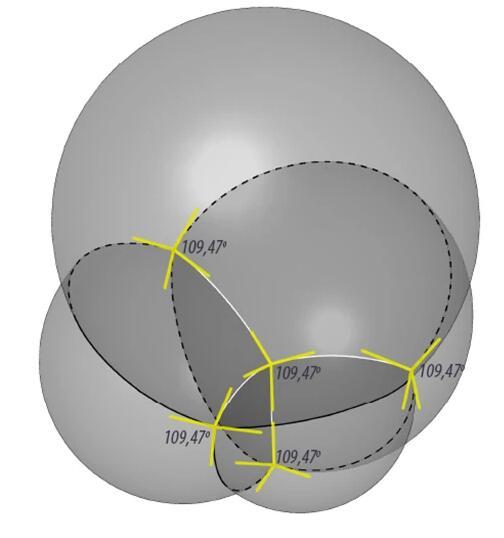
泡泡筏和泡泡堆中的連接方式是由誰決定的呢?大自然顯然比蜜蜂更會算賬。泡泡和皂膜是由水組成的(當然,表面有一層皂液分子),作用于液體表面的表面張力會拉動泡泡,讓其表面積盡可能的小。這就是為什么雨滴大致呈球形的原因,因為在相同體積下,球形的表面積是最小的;水滴在蠟質葉片上會縮成水珠,也是同樣的道理。


當水灑在疏水表面時,它可能會分裂成水滴。液滴的形狀最終由表面張力、重力和作用于水和水與固體表面之間的力決定。表面張力將液滴拉成大致的球形。如果后兩者更強,水滴就會像透鏡樣平鋪在表面上。如果疏水性不強,小水滴就會擴散成一層平坦光滑的薄膜。丨圖源:Stuchelova,Kuttelvaserov/Shutterstock;Olgysha/Shutterstock;Pitiya Phinjongsakundit/Shutterstock
現在我們知道了表面張力決定泡泡的連接方式,泡沫總會找到一種具有最小表面張力的結構,也就是使總表面積最小的結構。但是,關于泡沫的結構還需要考慮另一個問題,即力學上的穩定。在連接點處,沿著不同方向的作用力必須達到平衡。無論是泡泡筏的平鋪還是泡泡堆的四面相連,都是能滿足這一要求的連接方式。
有人認為,蜂巢也可以看作是蜂蠟凝固之后形成的“泡泡筏”,但這就無法解釋為什么造紙胡蜂(paper wasp,Polistes dominula)的蜂巢里也是六邊形組成。它們的窩可不是蜂蠟做的,而是它們自己的唾液與木材纖維、莖等混合咀嚼之后得到的糊狀“紙漿”。表面張力在其中起不到什么作用。而且,不同類型的黃蜂遺傳了不同的建筑設計能力,這種差別很明顯。

用自己分泌的柔軟蜂蠟搭建完美六邊形蜂巢,蜜蜂似乎是進化出了這種能力。但也有些研究者認為,柔軟的蜂蠟上本身存在的表面張力就足以把每個“小隔間”拉伸成特定的形狀,就像泡泡筏中的泡泡堆積一樣。丨圖源:Grafissimo/Getty
力學規律只告訴了我們泡泡之間的連接方式,卻沒有告訴我們泡沫里的每一個泡泡最終會形成什么形狀。仔細看,這些泡泡是具有不同形狀和大小的多面體,多面體的邊都不是筆直的直線,多少帶有一點點弧度;有的面有五條邊,有的面有六條邊,也有的只有四條甚至三條邊。這是因為泡泡內的氣體壓力與氣泡體積成反比,大氣泡旁邊的小氣泡會向外膨脹,發生輕微的彎曲,所以這些不同形狀的多面體都能通過適當的微調,形成四面相接的穩定結構。盡管它們遵守一些幾何規則,但也相當混亂。
有沒有那種所有泡泡都是一樣大小的“完美”泡沫堆呢?什么樣子的泡沫堆既能使得泡泡的表面積總和最小,又能在連接處滿足角度的要求呢?這個問題已經爭論了很多年。在很長一段時間內,人們認為理想的泡泡形狀是由6個正方形和8個正六邊形表面圍成的十四面體(截角八面體)。直到1993年,都柏林三一學院的兩位物理學家Denis Weaire和Robert Phelan發現了一種不那么規則、表面積卻更小的結構,它由8種不同形狀的泡泡重復排列而成。后來,這個略顯復雜的圖案出現在了2008年北京奧運會游泳館“水立方”的外立面上——它就是“水立方”泡沫圖案的設計靈感來源。
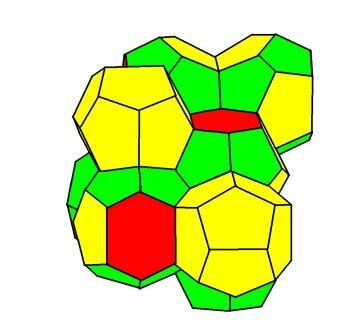
Weaire-Phelan的泡沫結構丨圖源:wiki
生物細胞中出現的一些圖形,也遵循了泡泡結構的形成機制。例如,蒼蠅的復眼是由一個個六邊形組合在一起的,就像泡泡筏中那樣;每一只小眼的感光細胞,也是四個四個地連接在一起,就像泡泡堆一樣。即使在發生了突變的蒼蠅身上,它們眼睛里每一組感光細胞不止四個,其排列方式仍然跟泡泡模式大致相同。


氣泡和泡沫在自然界中也有實際用途。圖中展示的是一種浮掛在海中生活的紫蝸牛,泡泡包裹著它們分泌的粘液形成浮筏使,它們以捕食生活在水面的小生物為生。丨圖源:Dorling Kindersley;Denis Riek
Part.3 表面張力塑造極小曲面
同樣由于表面張力,皂膜會沿著閉合的線框形成一個平整的薄膜——想想看,你在吹泡泡時,塑料圈上是不是出現了一層膜?如果線框被彎折,那么皂膜的表面也會跟著彎曲。皂膜最終成型的曲面,就是能覆蓋整個空間,并且是表面積最小的一種形狀。如果你是一名建筑師,你就可以從中學到怎樣用最省材料的方式建造屋頂。事實上,很多建筑師比如如弗雷·奧托(Frei Otto)確實會從皂膜那兒“偷師學藝”,他們青睞“極小曲面”在幾何造型上的美麗與優雅,當然也因為這樣做更省耗材。

德國建筑師、工程師弗雷·奧托致力于使用最少的材料進行設計,創造了眾多經典建筑。圖為建于1963年德國漢堡的國際園藝展館。圖源:Atelier Frei Otto Warmbronn
所謂“極小曲面”,是指平均曲率為零的曲面。在表面張力的作用下,每一個表面都在“追求”最小,不僅要讓表面積最小,也要讓平均曲率趨于最小。曲率,是表征彎曲程度的概念,彎曲得越劇烈,曲率就越大。曲率可以是正值(外凸),也可以是負值(內凹,或者說鞍形)。因此,只要正負曲率互相抵消,這個曲面的平均曲率就為零,從而成為一個極小曲面。
如果一個極小曲面可以把空間分隔成由各式通道按照一定規律組成的網絡系統,那么這個曲面就叫作周期性極小曲面。(這里的周期性是指一組結構不斷地重復出現,或者說整個圖形是有規律的。)這樣的曲面在19世紀被發現時,似乎只被當成了數學家搗鼓出來的玩具,但是現在我們知道,這是自然界用表面張力創造出來的絕妙規律。(值得注意的是,數學上證明極小曲面和物理上的構造并不等同。)
Part.4 當極小曲面出現在生物的細胞或外殼
從植物到魚類再到大鼠,它們的細胞中都能找到這種具有極小曲面的膜結構。至于這種膜結構的確切作用,也許是用來隔開不同的生化反應,避免相互影響;也許是為了用最少的材料創建最多的“工作表面”,之所以這么說,是因為膜表面分布有大量的酶或其他活性分子,能進行多種生化反應。暫且不管它的功能是什么,創造這種結構其實并不需要一套復雜的“基因說明書”,物理學規則自會搞定這一切。
有些種類的蝴蝶,例如歐洲的黃星綠小灰蝶(green hairstreak,Callophrys rubi)和寬絨番鳳蝶(emerald-patched cattleheart,Parides sesostris),其翅膀鱗片上就有一種周期性極小曲面——螺旋二十四面體(gyroid)。從曲面的凸起處和從其他結構處反射回來的光波之間會發生干涉,波長的變化也就意味著顏色的消失或出現。這就是翅膀鱗片產生顏色的特別技巧。


頭帕科的一種海膽(Cidaris rugosa)的外骨骼也包含多孔網狀的結構,這是另一種周期性極小曲面。外骨骼會長出長長的尖刺,主要成分跟白堊和大理石一樣,都是碳酸鈣。而這種多孔網狀的結構讓外骨骼既堅固又輕便,有點像制造飛機時使用的泡沫金屬。


Cidaris rugosa丨圖源:wiki;Christopher Mah/echinoblog
海膽是怎么用碳酸鈣這種堅硬、不易變形的礦物做成多孔網格的呢?顯然,它們應該先是用柔軟靈活的膜制作了一個內部互通的網狀模具,然后再讓堅硬的材料在模具內部結晶成型,成為類似于泡沫金屬的“泡沫礦物”。

阿式偕老同穴海綿(Euplectella aspergillum英文俗稱維納斯花籃)的多孔骨架,就像凝固的泡沫構成——礦物質就填充在泡狀軟組織的交界處周圍。圖源:Dmitry Grigoriev/Shutterstock
這個辦法還可以用來實現更復雜的目的。比如,光線在這種網狀結構中會發生多次反射,形成復雜迂回的反射路徑,這些泡沫礦物就像鏡子,可以用來控制或引導光線的傳播方向。鱗沙蠶(Aphrodita aculeata,一種海洋多毛類蠕蟲)就是這樣做的,它們的幾丁質外棘刺內含有中空的蜂巢式微管,這些看似像毛發的結構就成了天然可引導光線的光纖。它們可以根據光照方向改變身體顏色,這似乎就是它們震懾捕食者的手段。

鱗沙蠶因其體型和行動像老鼠,因此俗稱為“海鼠(sea mouse)”丨圖源:wiki
海膽和鱗沙蠶等先用軟組織或膜制作模具,再通過“澆鑄”過程在模具內部形成具有特定形狀的外骨骼的方法,即所謂的“生物礦化作用(Biomineralization)”,在海洋生物中屢見不鮮。例如,一些海綿動物的外骨骼看上去像是腳手架,那其實就是條狀礦物用這種方式連接起來的,而且,礦物“條”的連接處跟泡泡堆非常類似——如果表面張力塑造了這些結構,那就絕對不是巧合。
生物礦化作用在放射蟲和硅藻等海洋生物身上產生了無比瑰麗的視覺效果。一些放射蟲和硅藻的外骨骼擁有精妙無比的圖案:礦物組成了一個個六邊形和五邊形,而且排列得齊齊整整,你甚至可以管它們叫海中蜂巢。19世紀末,當德國生物學家(同時也是一名極具天賦的藝術家)恩斯特·黑克爾(Ernst Haeckel)第一次在顯微鏡下看到這些圖案時,震撼的畫面令他折服。驚嘆之余,他將這些圖案畫了下來,并出版了繪畫作品集《自然界的藝術形態》(Art Forms in Nature)。這部作品在20世紀初的藝術家之間非常有影響力,時至今日仍令人贊嘆。

“不僅是圖集,而是對世界觀的總結”,著名德國生物學史專家的Olaf Breidbach如此評價海克爾的作品。丨圖源:Ernst Haeckel,Kunstformen der Natur(1904).
在黑克爾看來,生物身上展現出來的這些圖案是大自然的神來之筆,可見大自然具有超乎想象的創造力和藝術表現力。當然,我們今天已經知道,這些圖案真正的“幕后推手”不是什么神祗的力量,而是表面張力,盡管如此,我們依然不能否認他觀念里的核心思想——
面對自然界創造出來的這些奇跡般的、無處不在的美麗,我們只有嘖嘖稱奇的份兒。










