合作客戶/
拜耳公司 |
同濟大學 |
聯合大學 |
美國保潔 |
美國強生 |
瑞士羅氏 |
相關新聞Info
液態Ag-O系表面張力和表面過剩量計算、氧氣壓力和溫度的預測模型——模型(二)
來源:過程工程學報李天骕 劉劍雄 單顯祥 李堪鵬 瀏覽 234 次 發布時間:2024-05-28
2理論模型
2.1液態Ag表面張力與溫度的關系
研究[20]表明,液態金屬的表面能與內聚能之間存在比例關系,表達式為:
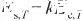 (1)
(1)
式中,Es,T和Ec,T分別表示溫度為T時的單位面積表面能(J/m2)和摩爾內聚能(J/mol);k為比例系數,其與表面相和本體相的原子配位數有關。
由于表面能和表面張力通常具有相同的大小和維度,在沒有嚴格區分的情況下,認為二者是等價的。根據式(1)可以得到液態Ag的表面張力與內聚能之間的關系式,即:
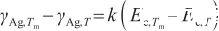 (2)
(2)
式中,γAg,T表示溫度為T時液態Ag的表面張力(N/m),Tm表示Ag的熔點(K),γAg,Tm和Ec,Tm分別表示熔點溫度下的表面張力和摩爾內聚能。其中,摩爾內聚能與溫度和定壓熱容有關,表達式為:
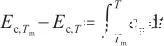 (3)
(3)
式中,cp表示定壓熱容[J/(mol·K)]。
當溫度升高到臨界溫度時,液態Ag完全轉變為氣態。此時,表面張力降低為0。根據式(2)和(3),可以得到:
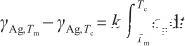 (4)
(4)
式中,Tc表示液態Ag的臨界溫度(K),γAg,Tc表示臨界溫度下的表面張力,并且γAg,Tc=0。由此得到比例系數k的表達式,即:
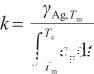 (5)
(5)
聯立式(2),(3)和(5),可以得到:
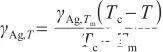 (6)
(6)
此外,表面張力是原子間作用力的宏觀表現,可表示為單位長度的力,取決于各個原子之間的作用力及單位長度上的原子數目。然而,式(6)僅反映了各個原子之間的作用力,并沒有涉及單位長度上的原子數目。考慮液態Ag熱膨脹對表面張力的影響,引入線膨脹系數α來描述液態Ag在膨脹過程中單位長度上原子數目的變化。因此,可以將式(6)變換為如下形式:
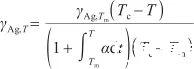 (7)
(7)
式中,α表示線膨脹系數(K-1)。
式(7)表示在整個溫度范圍內,液態Ag的表面張力與溫度的關系,相關參數的取值列于表1[21-26]。

表1模型計算中使用的物理參數[21-26]
Table 1 The physical parameters used in the model calculations[21-26]
通過對式(7)關于溫度T求導,可以得到液態Ag表面張力的溫度系數,其表達式為:
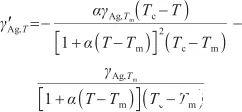 (8)
(8)
式中,γ?Ag,T表示液態Ag表面張力的溫度系數[N/(m·K)]。
從熱力學角度看,表面張力系數的負值表示為表面過剩熵SAg(T),即:
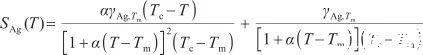 (9)
(9)
2.2液態Ag-O系的表面張力研究
對于液態Ag-O系,可以將其劃分為三個相,包括:氣相(g),指O2分子;本體相(b),表示液態Ag內部區域;表面相(s),位于氣相(g)和本體相(b)的交界處,具有一定的厚度。上述三個相的分布示意圖如圖1所示。
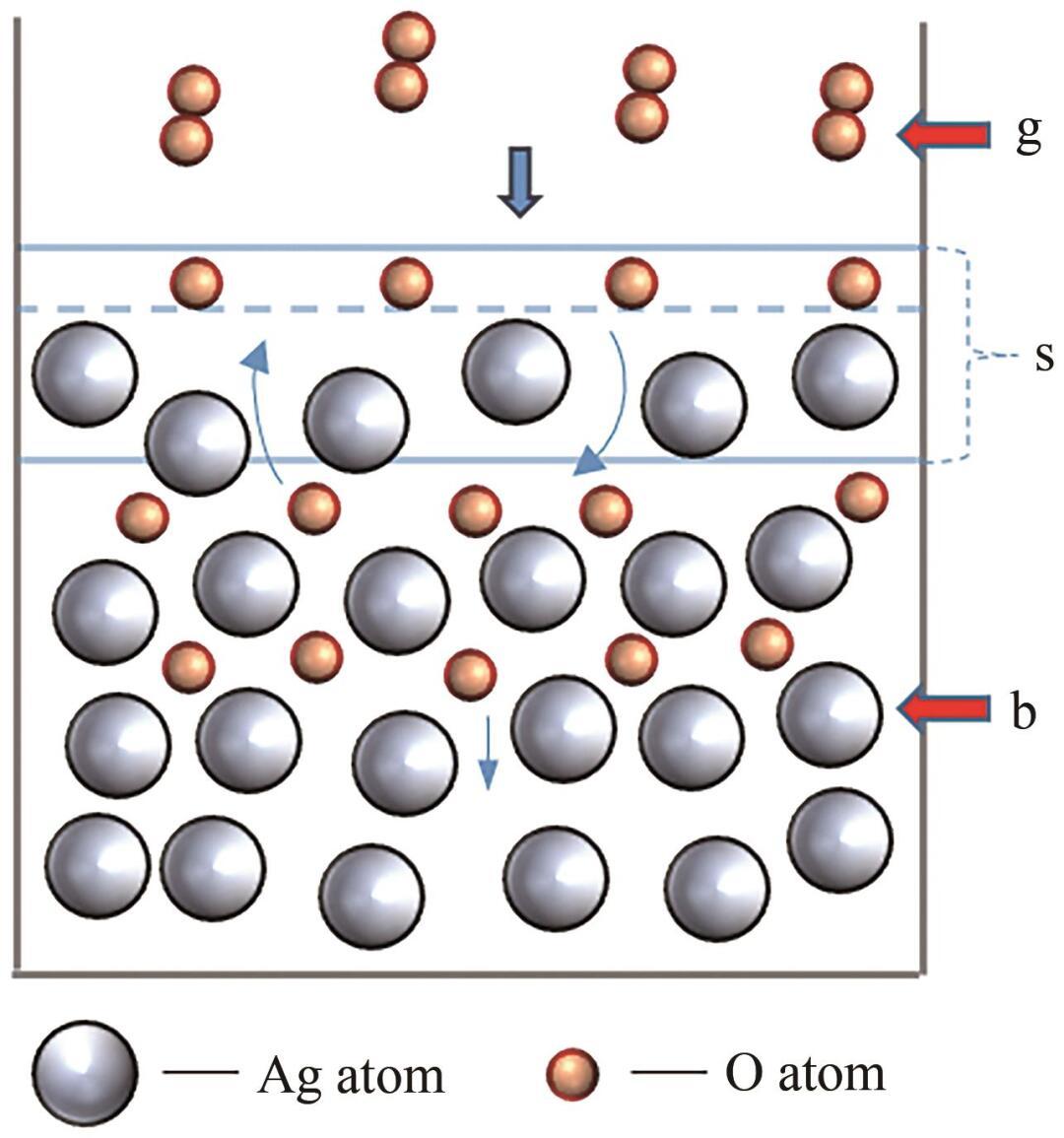
圖1 Ag-O系的相分布
根據圖1,首先O2分子從氣相(g)擴散至表面相(s);其次在Ag的催化下解離為O原子,并發生化學吸附;最后,O原子從表面相(s)擴散至本體相(b)。整個過程可以表示為:
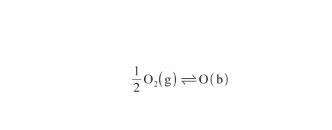 (10)
(10)
與此同時,本體相(b)中的O原子傾向富集于表面,以降低自由能。假設表面相(s)中的空位(V)數量有限,并且每個空位只能被一個O原子占據,則O原子的表面偏析過程可以表示為:
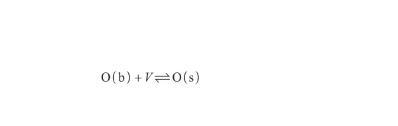 (11)
(11)
根據式(10)和(11),當系統的表面相(s)和本體相(b)之間達到熱力學平衡時,可以使用Butler方程[17]來描述表面張力,即:
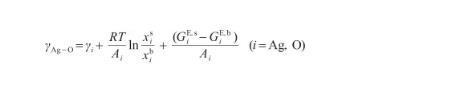 (12)
(12)
式中,γAg-O表示Ag-O系的表面張力(N/m),γi表示純組分i的表面張力(N/m),R為氣體常數[J/(mol·K)],x和x分別表示組分i在表面相和本體相中的摩爾分數(mol/mol),Ai為組分i的摩爾表面積(m2/mol),G和G分別表示表面相和本體相中組分i的偏摩爾過剩自由能(J/mol),并且G=λG,其中λ為表面相和本體相的原子配位數之比[27]。G可由摩爾過剩自由能GE,b表示,其關系式為:
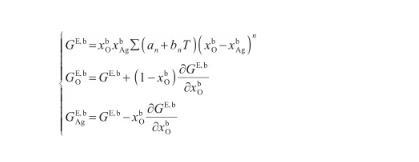 (13)
(13)
式中,GE,b表示Ag-O系的摩爾過剩自由能(J/mol),n,an和bn均為待定參數,可以通過相圖計算獲得。
另外,液態Ag的摩爾表面積AAg可以通過以下表達式[28]計算得到:
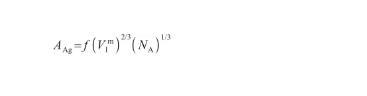 (14)
(14)
式中,V表示液態Ag的摩爾體積(m3/mol),NA為阿伏伽德羅常數(6.02×1023),f表示幾何因子(無量綱)。其中,V和f的計算式為:
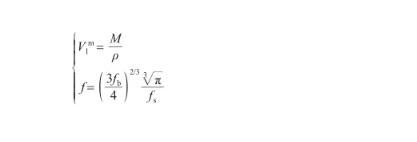 (15)
(15)
式中,ρ為液態Ag的密度(kg/m3),M為Ag原子的摩爾質量(kg/mol),fb和fs分別為本體相和表面相的原子堆積比率。表面相原子總是緊密排列,以達到自由能最小的狀態,通常認為其原子堆積比率與Ag(111)晶面相同[28],即fs=0.906;對于本體相,隨著溫度升高,體積逐漸增大而原子堆積比率相應降低。因此,fb的計算式為:
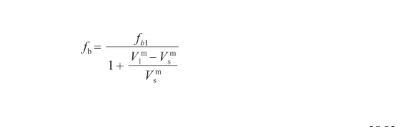 (16)
(16)
式中,fb1表示為本體相在熔點溫度下的原子堆積比率,且fb1=0.704[28];V表示固態Ag在熔點溫度下的摩爾體積(m3/mol)。
2.3 Butler方程的簡化
由式(12)和(13)可以看出,Butler方程計算較為復雜。考慮液態氧的表面張力很小[14],可以認為γO≈0。另外,由于Ag-O系中O原子數遠小于Ag原子數[29],可以將Ag-O溶體視為理想溶體。此時,GE,b=G=G=0。根據文獻[18],當式(12)所示的Butler方程用于描述理想溶液時,通過假設系統內兩組分具有相等的摩爾表面積,可以得到改進的Butler方程。這個改進的Bulter方程能夠推導出Gibbs吸附方程和Langmuir方程,被認為是表面張力和溶液吸附的根本方程。因此,令AAg=AO,將式(12)變換為:
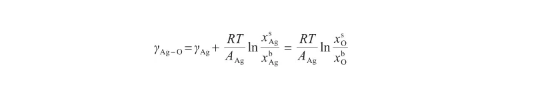 (17)
(17)
為了驗證這種近似處理的合理性,使用理想溶體近似模型計算Ag-O系的液相線,并將結果與實驗相圖進行比較。
對于Ag-O系,兩組元的原子百分數之和為1,即:
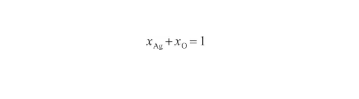 (18)
(18)
式中,xAg和xO分別為系統中Ag原子和O原子濃度(at%)。
液相線表示系統由液態轉變為固態的初始溫度或其逆過程的終了溫度。通過液態、固態中的Ag原子濃度來描述這一可逆過程,從而有:
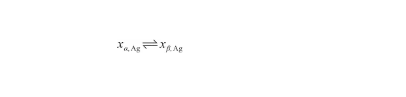 (19)
(19)
式中,xβ,Ag和xα,Ag分別表示Ag-O系液態、固態中的Ag原子濃度(at%)。
Ag-O系固-液轉變過程進行到一定限度時,系統達到平衡,自由能不再發生變化,且為最小。同時,固態、液態中的Ag原子濃度也不再發生變化,平衡系數KI表示為:
 (20)
(20)
根據Van't Hoff方程,平衡系數KI與反應焓變之間有如下關系:
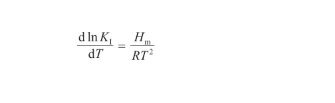 (21)
(21)
式中,Hm為Ag的摩爾熔化熱(J/mol)。
將式(20)代入式(21)中,并對溫度從T到Tm積分,得:
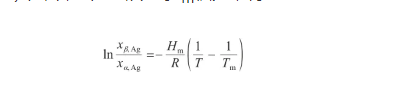 (22)
(22)
式中,Tm為Ag的熔點(K)。
由于固態Ag的溶氧量接近于0,可以認為xα,Ag≈1。聯立式(18)和(22),得:
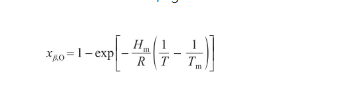 (23)
(23)
式中,xβ,O為液態Ag-O系中的O原子濃度(at%)。
根據式(23)計算了Ag-O系的液相線,結果如圖2所示。從圖中可以觀察到,理想溶體近似模型的計算值與實驗相圖[29]非常吻合。因此,可以將Ag-O系視為理想溶體。
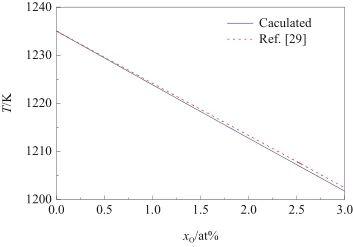
圖2 Ag-O系液相線
聯立式(17)和(18),將Ag原子濃度代以O原子濃度,從而有:
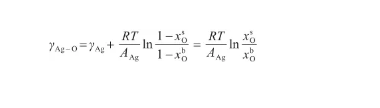 (24)
(24)
根據式(24),可以將表面相的O原子濃度x表示為:
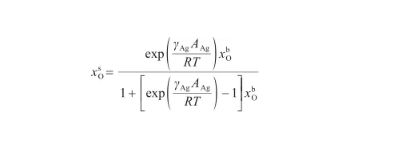 (25)
(25)
由于式(25)與改進的Langmuir方程[30]具有相同的形式,因此將其變換為:
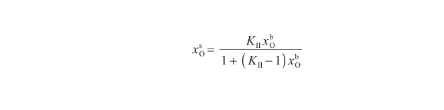 (26)
(26)
其中,KII表示表面偏析平衡系數[18],表達式為:
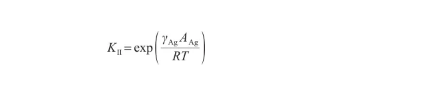 (27)
(27)
將式(26)代入式(24),可以得到液態Ag-O系的表面張力關于溫度和O原子濃度的表達式,即:
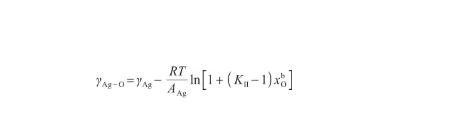 (28)
(28)
根據Sieverts定律[31],Ag-O系的飽和O氧原子濃度與氧氣壓力的平方根成正比,即:
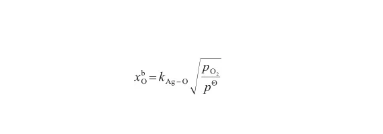 (29)
(29)
式中,kAg-O為Ag-O系的Sieverts系數,是溫度的函數;pO2表示氣相的氧氣壓力(kPa),pΘ表示標準大氣壓(101 kPa)。
顯然,式(10)中的平衡系數與式(29)中的Sieverts系數相等。因此,可以得到Sieverts系數與標準吉布斯自由能變之間的關系式,即:
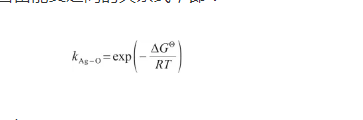 (30)
(30)
式中,ΔGΘ表示液態Ag溶氧過程的標準吉布斯自由能變(J/mol),其計算式[29]為:將式(30)代入式(29)中,得:
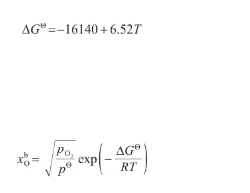 (31)(32)
(31)(32)
結合式(28)和(32),可以得到液態Ag-O系的表面張力關于溫度和氧氣壓力的表達式,即:
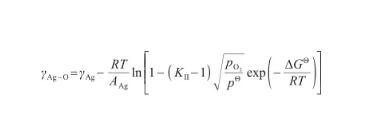 (33)
(33)
2.4液態Ag-O系表面的氧吸附行為
根據Gibbs吸附方程,表面過剩量的定義式為:
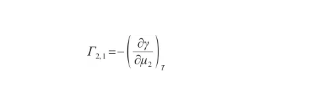 (34)
(34)
式中,Γ2,1表示二元系中組分2相對于組分1的表面過剩量(mol/m2),μ2為組分2的化學勢(J/mol)。
通過對式(28)關于x求偏導,可以得到:
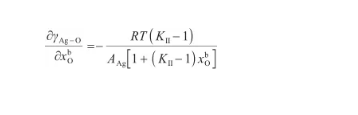 (35)
(35)
在液態Ag-O系中,O原子的化學勢(μO)表示為:
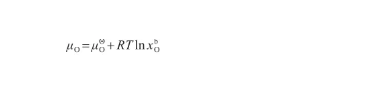 (36)
(36)
其中,μ表示O原子的標準化學勢(J/mol)。對式(36)關于x求偏導,得:聯立式(35)和(37),得:
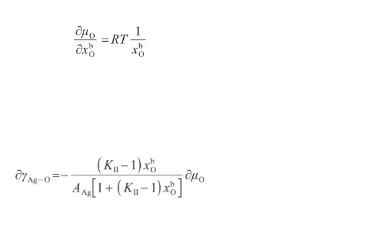 (37)(38)
(37)(38)
結合式(34)和(38),可以得到O原子的表面過剩量,表達式為:
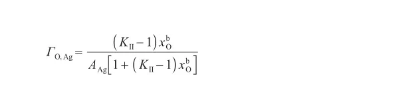 (39)
(39)
將式(32)代入式(39)中,可以得到表面過剩量關于溫度和氧氣壓力的表達式,即:
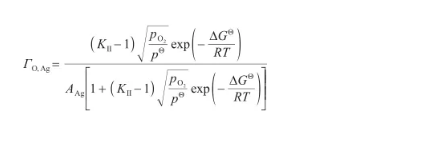 (40)
(40)
此外,在式(26)左右兩邊同時除以x,得到表面偏析因子(η)的表達式。結合式(32),將其變換為:
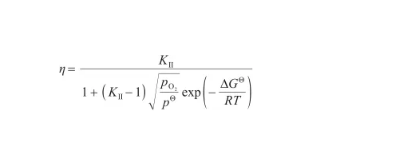 (41)
(41)
液態Ag-O系表面張力和表面過剩量計算、氧氣壓力和溫度的預測模型——摘要 、簡介










