合作客戶/
拜耳公司 |
同濟大學 |
聯合大學 |
美國保潔 |
美國強生 |
瑞士羅氏 |
相關新聞Info
熱力學模型計算MgO-B2O3-SiO2-CaOAl2O3富硼渣表面張力(二)
來源:中國有色金屬學報 瀏覽 85 次 發布時間:2024-08-13
2 MgO-B2O3-SiO2-CaO-Al2O3體系熔渣表面張力模型的建立
Butler假設熔體表面相內組分與體相內組分在熱力學上都達到平衡,推導出表面張力與熱力學性質之間的關系(Butler方程)。本模型基于Butler方程計算熔渣表面張力,熔渣表面相和體相內組分通過熔渣結構離子與分子共存理論來確立。本模型主要假設如下:1)熔渣表面相與體相都遵守熔渣結構離子與分子共存理論,即組元結構都由簡單離子、分子和復合分子組成,熔渣表面相和體相中簡單離子和分子進行著形成復合分子的動力學質量平衡反應,且表面相和體相中形成復合分子的反應都遵守質量作用定律;2)熔渣表面相和體相中各組元的質量作用濃度和熔渣表面張力符合Butler方程:
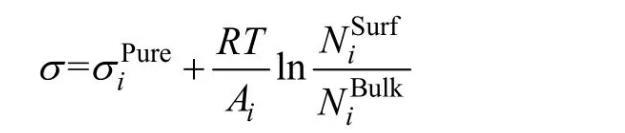
式中:σipure表示純組元和Al2O3)的表面張力;Ai為純組元i的摩爾表面積,其中L為校正因子,熔渣中設為1.091;N0為阿伏加德羅常數,Vi為組元i的摩爾體積);R和T分別表示摩爾氣體常數和絕對溫度;為組元i在表面相或體相的質量作用濃度。
根據共存理論以及上述確定的MgO-B2O3-SiO2-CaO-Al2O3富硼渣體系熔渣中存在的結構單元,定義熔渣中成分分別為。結構組元作用濃度符號表示為:
所有組元總平衡摩爾數表示為∑ni。各組元作用濃度表達式為:
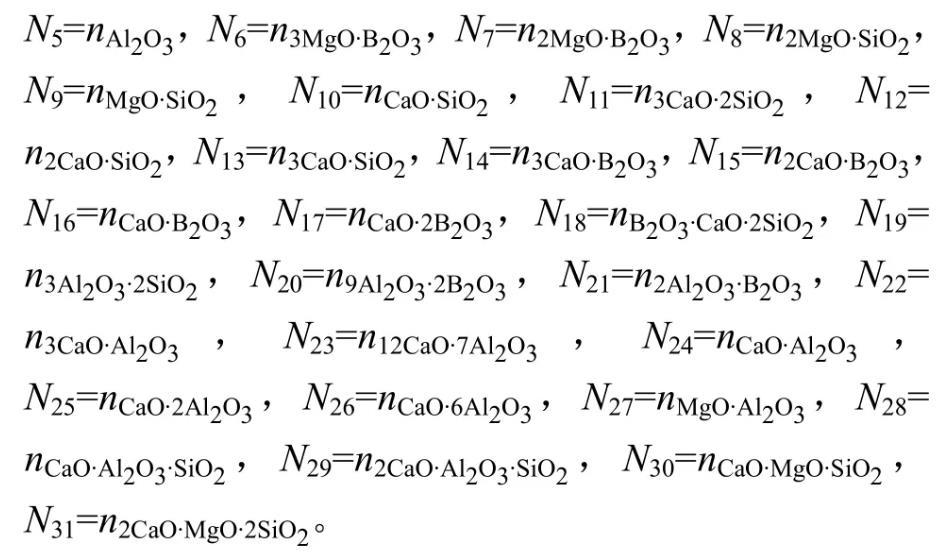
在1773~1873 K溫度范圍內,熔渣中各組分之間形成復雜分子的反應式及其達到平衡時的標準Gibbs自由能(以純物質為標準態)和質量作用濃度的表達式如表1所列,其中所有反應的平衡常數可通過的關系式進行計算。
MgO-B2O3-SiO2-CaO-Al2O3渣系中質量平衡公式如下:
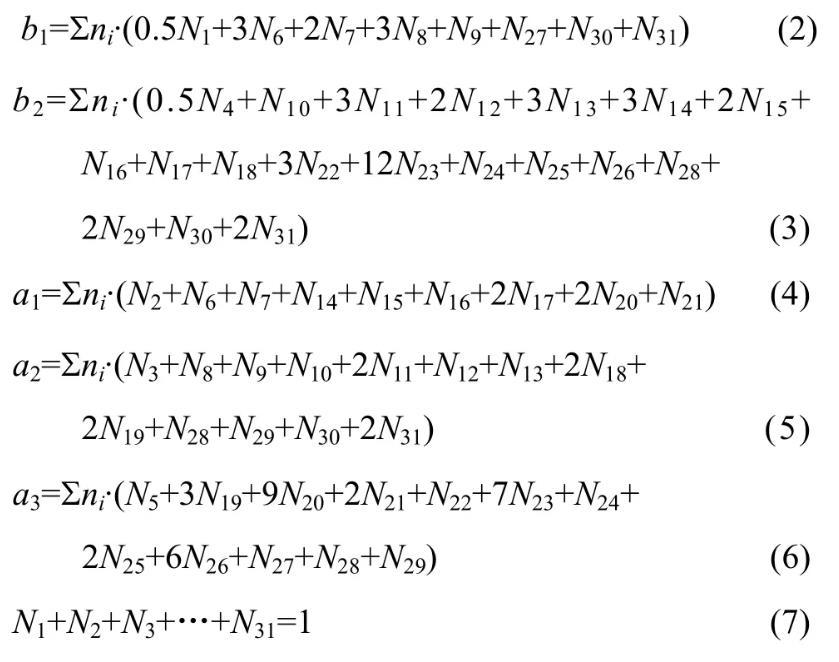
因此,由表1和式(2)~(7)建立計算MgO-B2O3-SiO2-CaO-Al2O3渣系中結構組元和離子對作用濃度Ni的控制方程,其中N6~N31由N1~N5表示出來。在一定溫度下,熔渣成分代入該方程組,采用迭代法計算出所有結構組元和離子對的作用濃度。
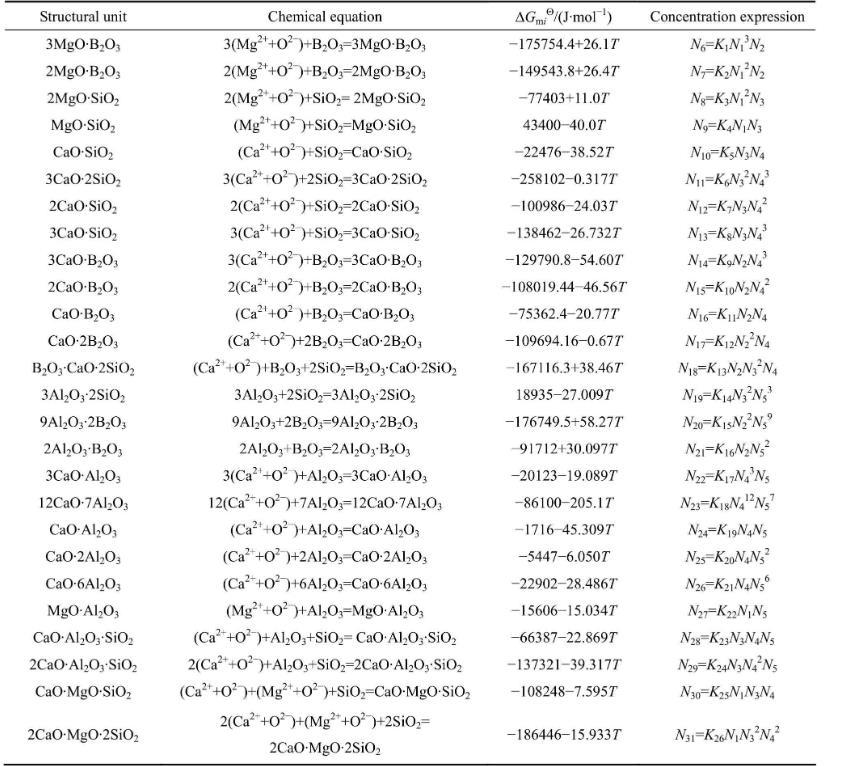
表1 MgO-B2O3-SiO2-CaO-Al2O3渣系中復雜分子的化學反應及標準Gibbs自由能和作用濃度的表達式
對于MgO-B2O3-SiO2-CaO-Al2O3體系,依據Bulter方程,其表面張力可以分別表示為
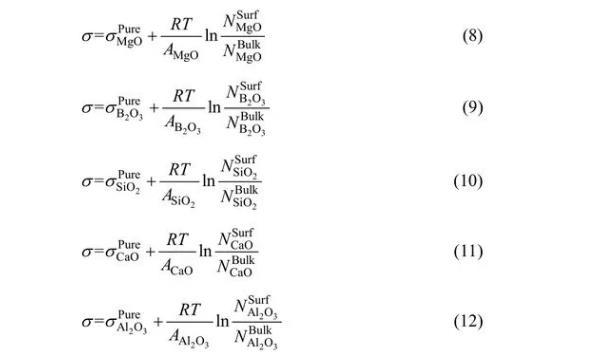
依據上述描述,建立模型可計算熔渣表面張力,其中,NiBulk可以通過熔渣成分的摩爾分數和基于熔渣結構離子與分子共存理論的形成復合分子的化學平衡計算得出。然后進一步基于共存理論和Butler方程,通過已知量NiSurf、σiPure和Ai,利用方程(8)~(12)可計算出σ和NiSurf值。MgO-B2O3-SiO2-CaO-Al2O3渣系中σiPure和Ai數據可見表2和3。
3計算結果及討論
3.1表面張力的計算值與實測值對比
為了驗證本模型計算結果的準確性,需將計算結果與文獻實驗數據進行對比。富硼渣相關體系中,已有B2O3-CaO體系、B2O3-SiO2-CaO體系、B2O3-CaOAl2O3體系、B2O3-SiO2-CaO-Al2O3體系和MgOB2O3-SiO2-CaO-Al2O3體系的表面張力實驗數據的報道,相關體系的組分范圍及溫度范圍如表4所列。本研究中計算了上述體系的表面張力計算值,并與文獻實驗數據進行了對比,對比結果如圖1和表4所示。5個體系文獻實驗結果與計算結果總平均相當誤差為9.03%。大多數熔渣的表面張力實驗誤差一般為±5%~10%,由此可知,本模型計算的熔渣表面張力值與實驗值吻合較好。比較結果顯示,B2O3-SiO2-CaO體系和B2O3-CaO-Al2O3體系偏差較大,這一方面可能與表面張力高溫測量難度和精度導致的誤差有關,另一方面本模型未考慮熔渣中部分組元會存在飽和現象。由于氧化物純物質的熔點偏高,計算溫度下采用的氧化物純組分表面張力數據由已有純物質的實驗數據進行合理的外推得到,這些也可能對模型計算結果帶來一定的誤差。
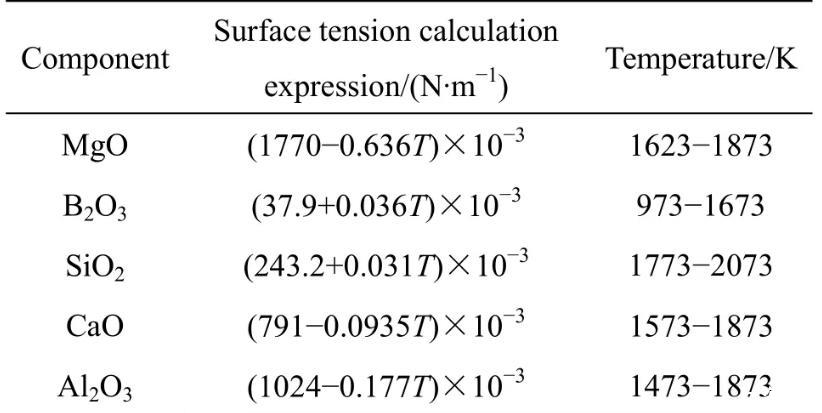
表2純組元表面張力與溫度的關系

表3純組元摩爾體積與溫度的關系
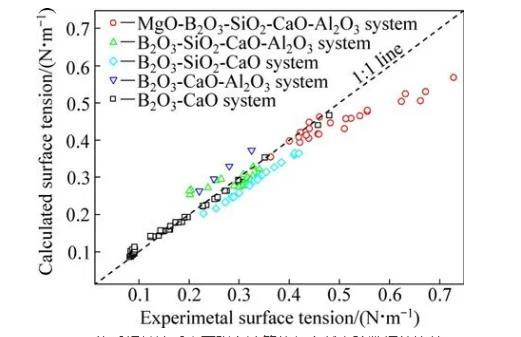
圖1 MgO-B2O3-SiO2-CaO-Al2O3體系相關渣系表面張力計算值與文獻實驗數據的比較
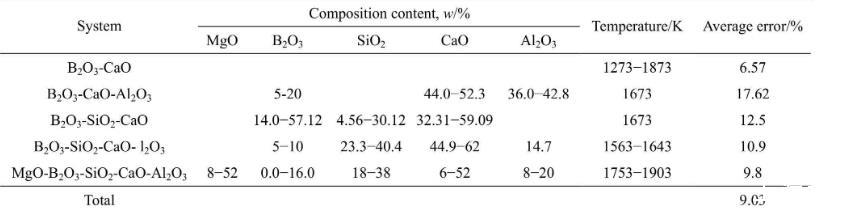
表4富硼渣相關實驗渣系組分、溫度及相對平均誤差
熱力學模型計算MgO-B2O3-SiO2-CaOAl2O3富硼渣表面張力(一)










